Содержание
Предварительный опрос
- картинка для показа всему классу на маркерной доске.
Упражнения
Упражнение в браузере - интерактивное упражнение, для которого потребуется бесплатный веб-плеер АвтоГрафа и любой веб-браузер
Упражнения в АвтоГрафе - интерактивные упражнения на закрепление полученных знаний, которые выполняются в программе АвтоГраф
Видеоурок содержит примеры использования АвтоГрафа при изучении квадратных уравнений
Полезные советы - пошаговая инструкция по созданию демонстрации,
показывающей, как коэффициенты квадратного уравнения влияют на его график
Предварительный опрос
Быстрый предварительный опрос поможет выявить пробелы в знаниях учеников и скорректировать план урока.
Покажите классу эту картинку, дайте 30 секунд на размышление, а затем попросите поднять пальцы: 1 - за А, 2 - за B и т.д.
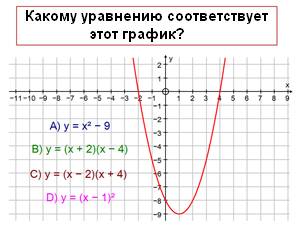
Упражнения
Упражнения в браузере
Чтобы работать с веб-упражнениями АвтоГрафа, сам АвтоГраф не нужен, достаточно его бесплатного плеера.
Краткая инструкция по установке плеера
Задание: найдите формулу кривой
Упражнения в АвтоГрафе
Для выполнения этих упражнений требуется программа АвтоГраф. Скачать ее пробную 29-дневную версию
вы можете здесь. Купить программу можно на
веб-странице интернет-магазина Института новых технологий.
Упражнения этого раздела нацелены на закрепление полученных знаний.
Упражнение 1 - Рисуем графики квадратичных функций
Загрузите файл чертежа
1. Sketching Quadratics.agg.
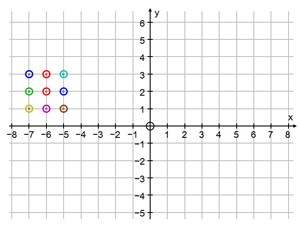
Это упражнение поможет ученикам научиться быстро и правильно строить графики квадратичной функции.
Откройте файл упражнения на маркерной доске.
Попросите учеников ответить на вопросы:
1. В каких точках график уравнения y = x2 - 4 пересекает ось X?
2. В каких точках этот график пересекает ось y?
3. В какой точке расположен минимум этой функции?
4. Назовите координаты любой другой точки этого графика, например, чему равен y при x = 1?
Когда ответы будут получены, попросите кого-нибудь из учеников подойти к маркерной доске и отметить все эти точки при помощи расположенных на чертеже цветных кружков.
После этого проверьте решение, введя уравнение y = x2 - 4 в окне Ввод уравнения...  .
Вы можете использовать этот метод и для изучения особенностей любой другой квадратичной функции - попробуйте предложить ученикам создать свою собственную квадратичную
функцию и найти ее характерные точки.
Упражнение 2 - Различные формы записи квадратичных функций
Загрузите файл чертежа
2. Different Forms of Quadratics.agg
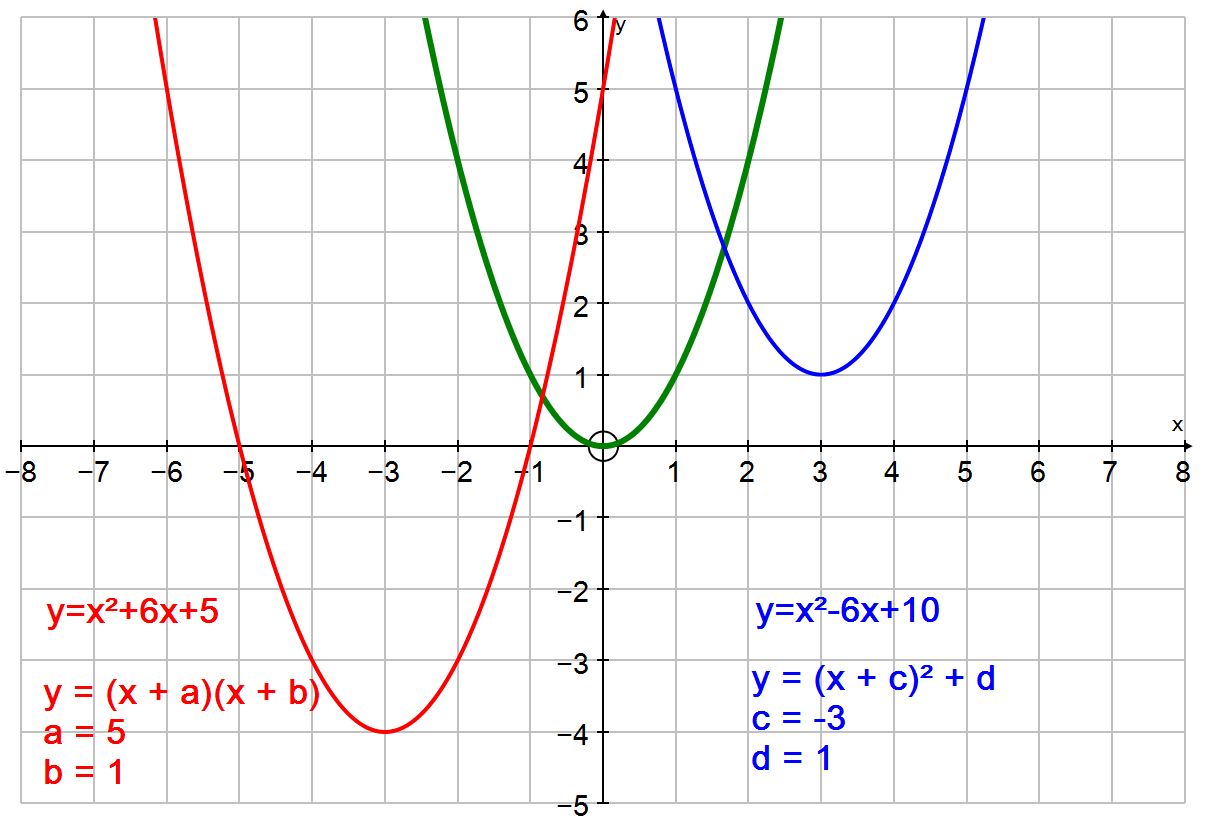
Это упражнение познакомит учеников с различными формами записи квадратных уравнений.
Зеленая кривая соответствует функции y = x2 и используется для сравнения.
Красная кривая - график квадратного уравнения, записанного в виде произведения двух сомножителей: y = (x + a)(x + b)
Синяя кривая - график квадратного уравнения, заданного в виде двух слагаемых: y = (x + c)2 + d
Вопросы и задания:
1. Как каждая константа влияет на вид графика?
2. Меняя значение постоянных c и d, наложите синюю кривую на красную.
3. Меняя значение постоянных а и b, попробуйте наложить красную кривую на синюю.
Объясните, почему это невозможно.
Чтобы изменять значение постоянных a, b, c и d, ученики должны
использовать инструмент Управление константами
Упражнение 3 - Дискриминант
Загрузите файл чертежа
3. The Discriminant.agg
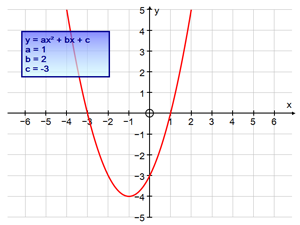
Это упражнение можно использовать, чтобы показать, как значение дискриминанта квадратного уравнения влияет на его график.
В упражнении задан график функции y = x2 +2x - 3, где a = 1, b = 2 и c = -3
Вопросы и задания:
1. Как с помощью этого графика можно найти решение квадратного уравнения?
2. Вычислите значение дискриминанта b2 - 4ac
3. Используя инструмент Управление константами  ,
установите несколько других значений постоянных a, b и c и определите для них значение дискриминанта.
4. Найдите такое сочетание постоянных, при которых дискриминант имеет отрицательное значение.
В чем особенность уравнения с таким дискриминантом?
5. Найдите такое сочетание постоянных, при которых дискриминант равен нулю. Какой вид при этом примет график?
В чем особенность уравнения с таким дискриминантом?
6. На основе этих экспериментов сделайте вывод о том, как по значению дискриминанта можно судить о виде графика квадратного
уравнения.
Упражнение 4 - Квадратичная зависимость
Загрузите файл чертежа
4. A Quadratic Relationship.agg
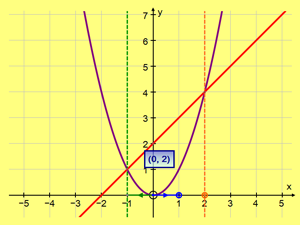
Идея этой задачи была найдена в старом учебнике геометрии.
Сначала была построена парабола y = x2. Затем - прямая, проходящая через следующие точки:
• первая точка - это пересечение параболы с оранжевой вертикальной линией,
проходящей через оранжевую точку на оси X.
• вторая точка - пересечение параболы с вертикальной зеленой линией, проходящей через точку,
симметричную синей точке на оси x.
Строго говоря, точка пересечения зеленой вертикали с осью X получена инверсией синего вектора.
И, наконец, на чертеже показаны координаты точки пересечения этой прямой с осью Y.
Задания и вопросы:
1. Подвигайте оранжевую и синюю точки вдоль оси Х.
Попробуйте определить, как координаты точки пересечения прямой с осью Y связаны с координатами синей и оранжевой точек.
Чтобы рассмотреть детали чертежа, вышедшие за пределы окна программы, используйте инструмент Перетащить
 .
2. Попробуйте найти уравнение, описывающее связь между координатами этих точек.
Видеоурок
В этом видеофильме - некоторые примеры использования АвтоГрафа при изучении квадратных уравнений.
Полезные советы
Вот действия, которые можно считать стандартными для того, чтобы показать, как коэффициенты квадратного уравнения влияют на его график:
Откройте АвтоГраф в Стандартном режиме.
Введите уравнение y = ax2 + bx + c. На чертеже появится график параболы.
Нанесите на этот график три точки.
Выделите эти точки, сделайте правый щелчок и выберите из появившегося меню пункт Парабола (3 точки). Поверх исходной параболы появится
новая парабола.
Выделите эту новую параболу.
Щелкните на значке Надпись и нажмите кнопку ОК. Появится текстовое окно с уравнением.
Теперь, используя инструмент Управление константами, меняйте значения a, b и c. Вы
увидите, как одновременно меняется и уравнение, и его график!
|
|
|
|
АвтоГраф - виртуальный конструктор по основным разделам
школьной математики. Предназначен для графического отображения
математических объектов в одномерном, двумерном и трехмерном
виде - геометрических фигур, графиков уравнений, представления результатов статистической обработки наборов данных.
Видеоролик
АвтоГрафа на сайте ИНТ.
Квадратичные функции - не самая актуальная
тема для Вас сегодня?
АвтоГраф можно использовать
и в других разделах школьной
математики:
- Функции и графики
- Векторы и переносы
- Системы (пространственных)
координат
- Уравнения и системы уравнений
- Параметрические уравнения
- Теория вероятности и элементы
статистики
- Геометрия, тригонометрия,
стереометрия
- Дифференцирование
и интегрирование
Англоязычные ресурсы Интернета
Mr Barton's Autograph Activities
(Веб-упражнения мистера Бартона, не требующие установки АвтоГрафа) <англ. яз>
Videotutorials
(Серия обучающих видеороликов) <англ. яз>
Autograph Training Material 2012
(Инструкции для начинающих пользователей АвтоГрафа) <англ. яз>
WorkSheets by Alan Catley
(Коллекция рабочих листов для ученика, разработанная Аланом Кэтли) <англ. яз>
Видеоуроки на английском языке, созданные
Крейгом Бартоном (Craig Barton),
Дугласом Батлером (Douglas Butler) и
Хасаном Лакисс (Hassan Lakiss).
Autograph Activities (Книги с упражнениями для АвтоГрафа) <англ. яз>
Твиттер АвтоГрафа
АвтоГраф на Фейсбуке
АвтоГраф в YouTube
Сайт АвтоГрафа <англ. яз>
Полный список англоязычных интернет-ресурсов на сайте Дугласа Батлера (Douglas Butler).
Программные продукты ИНТ
Математика
АвтоГраф
Живая Математика
Живая Статистика
Интерактивная Стереометрия
ЛогоМиры Вероятности
Математический кружок
Мат-Решка 1-4
Другие предметы
|
КВАДРАТНЫЕ УРАВНЕНИЯ
